三种红包分配算法实现

本文中，我将介绍几种主流的手气红包分配算法。

普通随机

用当前红包余额作为最大区间进行随机，这样做的好处是算法实现简单，但可能不均匀。如果第一个人随机到接近红包余额的金额，那么接下来的人就没得玩了。

流程图

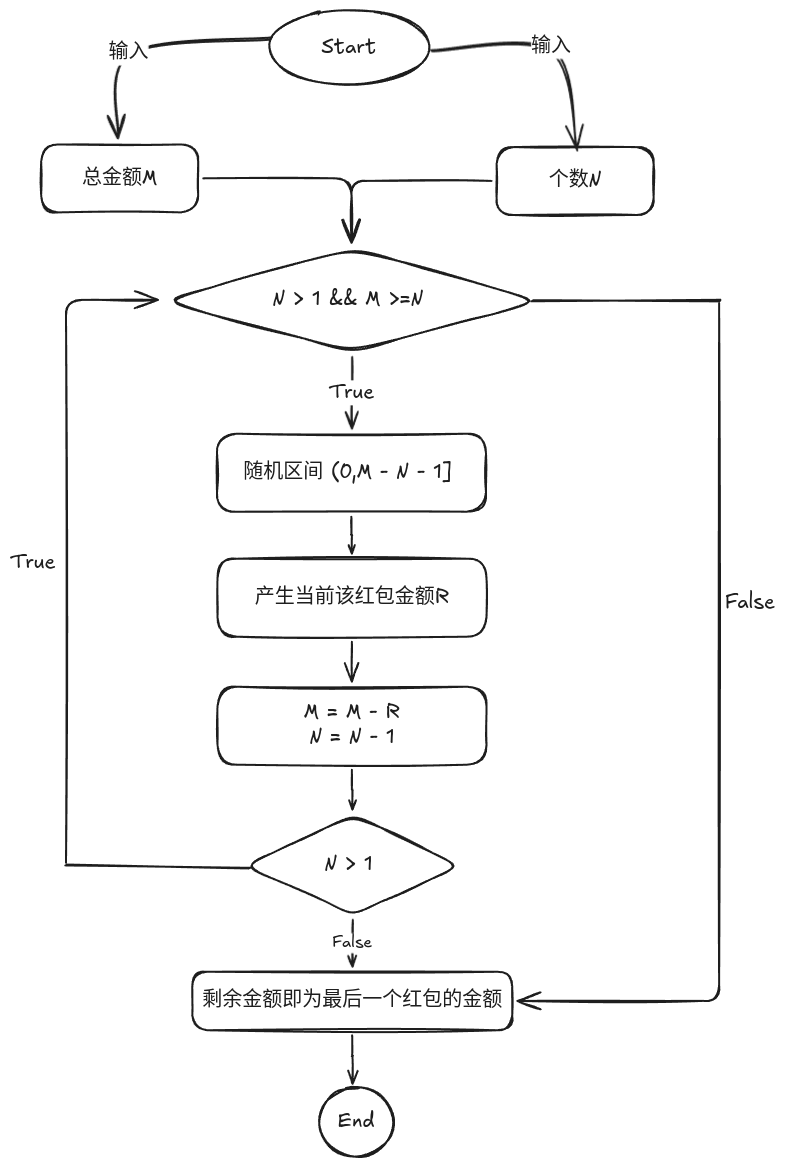
代码

// LeftMoneyRedBag 红包算法
//
//	money 红包金额 单位分
//	userNum 红包人数
//	返回红包金额 数组
func LeftMoneyRedBag(money, userNum int) ([]int, error) {
	// 检查参数
	if money <= 0 {
		return nil, errors.New("红包金额必须大于0")
	}
	if userNum <= 0 {
		return nil, errors.New("红包人数必须大于0")
	}
	if money < userNum {
		return nil, errors.New("不足以每个人发一分钱红包")
	}
	result := make([]int, userNum)

	if userNum == 1 {
		result[0] = money
		return result, nil
	}

	if money == userNum {
		for i := 0; i < userNum; i++ {
			result[i] = 1
		}
		return result, nil
	}

	// 初始化随机数种子
	rand.NewSource(time.Now().UnixNano())
	leftMoney := money
	leftUserNum := userNum

	// 随机分配金额
	for i := 0; i < userNum-1; i++ {
		// 保证每个红包最少分配 1 分，最大为 剩余金额 - (剩余红包数 - 1) * 1 分
		// 左闭右开
		maxTemp := leftMoney - leftUserNum
		money := rand.Intn(maxTemp) + 1
		result[i] = money
		leftMoney -= money
		leftUserNum--
	}

	// 最后一个红包的金额等于剩余的所有金额
	result[userNum-1] = leftMoney
	return result, nil
}

在较大的红包金额+人数的情况下，会出现前面的人普遍抢到的金额大，后面的人金额小的规律。

二倍均值

这里参看微信的红包算法，是这样描述的：

首先，如果红包只有一个，本轮直接使用全部金额，确保红包发完。
然后，计算出本轮红包最少要领取多少，才能保证红包领完，即本轮下水位；轮最多领取多少，才能保证每个人都领到，即本轮上水位。主要方式如下：
计算本轮红包金额下水位：假设本轮领到最小值1分，那接下来每次都领到200元红包能领完，那下水位为1分；如果不能领完，那按接下来每次都领200元，剩下的本轮应全部领走，是本轮的下水位。
计算本轮红包上水位：假设本轮领200元，剩下的钱还足够接下来每轮领1分钱，那本轮上水位为200元；如果已经不够领，那按接下来每轮领1分，计算本轮的上水位。
为了使红包金额不要太悬殊，使用红包均值调整上水位。如果上水位金额大于两倍红包均值，那么使用两倍红包均值作为上水位。换句话说，每一轮抢到的红包金额，最高为两倍剩下红包的均值。
最后，获取随机数并用上水位取余，如果结果比下水位还小，则直接使用下水位，否则使用随机金额为本轮拆到金额。

简单的来说就是：在就剩下一个红包的情况时，上下水位都为剩余金额；如果不是这种情况，上水位为两倍的剩余红包均值（2 * 当前剩余金额 / 当前剩余红包个数）。

流程图

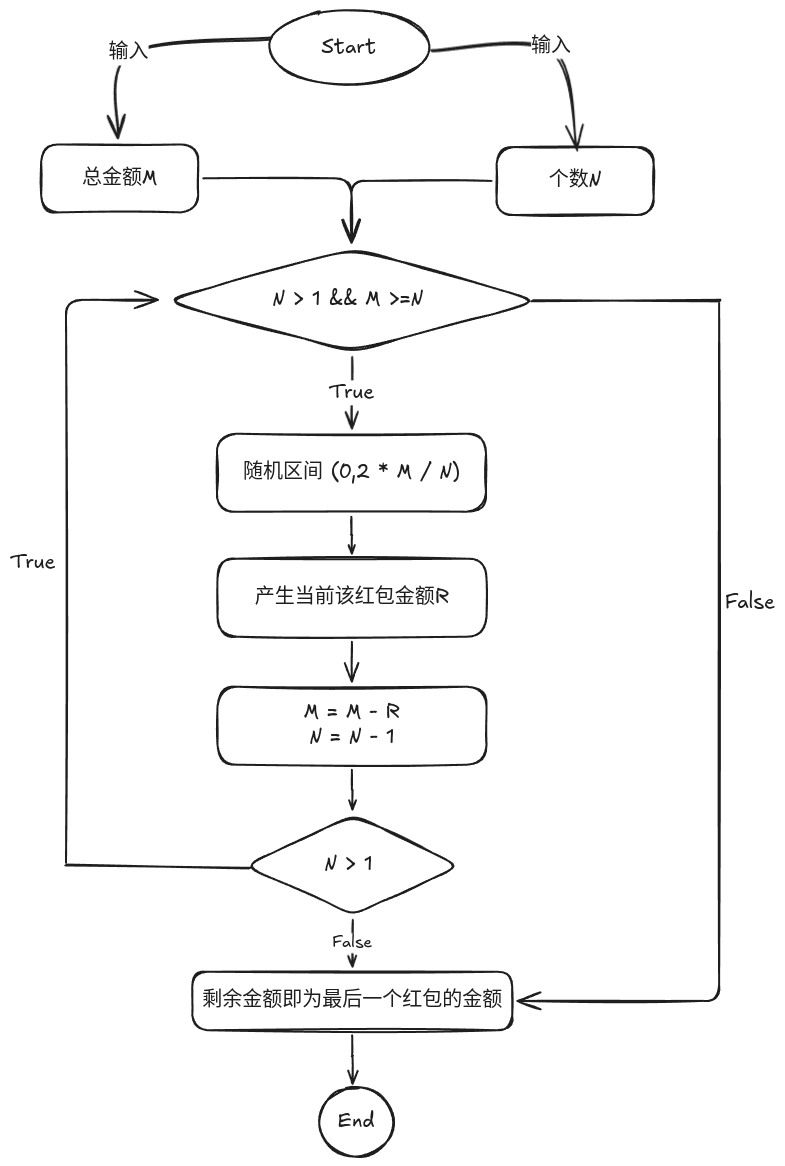
代码

// doubleMeanRedBag 红包算法
//
//	money 红包金额 单位分
//	userNum 红包人数
//	返回红包金额 数组
func doubleMeanRedBag(money, userNum int) ([]int, error) {
	// 检查参数
	if money <= 0 {
		return nil, errors.New("红包金额必须大于0")
	}
	if userNum <= 0 {
		return nil, errors.New("红包人数必须大于0")
	}
	if money < userNum {
		return nil, errors.New("不足以每个人发一分钱红包")
	}
	result := make([]int, userNum)

	if userNum == 1 {
		result[0] = money
		return result, nil
	}
	if money == userNum {
		for i := 0; i < userNum; i++ {
			result[i] = 1
		}
		return result, nil
	}

	// 初始化随机数种子
	rand.NewSource(time.Now().UnixNano())
	leftMoney := money
	leftUserNum := userNum

	// 随机分配金额
	for i := 0; i < userNum-1; i++ {
		// 两倍红包均值
		maxTemp := 2*leftMoney/leftUserNum - 1
		tempMoney := rand.Intn(maxTemp) + 1
		result[i] = tempMoney
		leftMoney -= tempMoney
		leftUserNum--
	}

	// 最后一个红包的金额等于剩余的所有金额
	result[userNum-1] = leftMoney
	return result, nil
}

二倍均值算法可以避免随机生成的金额，部分人金额过高，导致剩余的人的金额过小的尴尬。

线段分割

线段分割的实现逻辑会更复杂一些。

红包金额如果想随机分成 N 份，可以理解为：一个线段，随机选择 N-1 点进行切割。

代码

每次新产生的切割点都要和已有的切割点去进行比较是否已存在, 越往后这种方法的效率越低。我这里改进了一下。

// lineSegmentRedBag 线段切割法
//
//	money 红包金额 单位分
//	userNum 红包人数
//	返回红包金额 数组
func lineSegmentRedBag(money, userNum int) ([]int, error) {
	// 检查参数
	if money <= 0 {
		return nil, errors.New("红包金额必须大于0")
	}
	if userNum <= 0 {
		return nil, errors.New("红包人数必须大于0")
	}
	if money < userNum {
		return nil, errors.New("不足以每个人发一分钱红包")
	}
	result := make([]int, userNum)

	if userNum == 1 {
		result[0] = money
		return result, nil
	}
	if money == userNum {
		for i := 0; i < userNum; i++ {
			result[i] = 1
		}
		return result, nil
	}

	//构建随机数种子
	rand.NewSource(time.Now().UnixNano())
	//切点的数量
	pointsNum := userNum
	//切点数组
	points := make([]int, pointsNum)

	// 构建线段 0 - money 长度的线段，每个线段长度为 1
	line := make([]int, money)
	lineLen := money
	for i := 0; i < money; i++ {
		line[i] = i
	}
    // 这里使用数组, 利用下标的偏移
	for i := 0; i < pointsNum; i++ {
		index := rand.Intn(lineLen-1) + 1
		points[i] = line[index]
		line[index] = line[lineLen-1]
		lineLen--
	}

	//fmt.Printf("%v\n", points)

	// 排序
	sort.Ints(points)

	// 计算每个红包的金额
	for i := 0; i < userNum-1; i++ {
		if i == 0 {
			result[i] = points[i]
		} else {
			result[i] = points[i] - points[i-1]
		}
	}

	// 最后一个红包的金额等于剩余的所有金额
	result[userNum-1] = money - points[userNum-2]

	return result, nil
}

三种算法的对比

在1000000次循环下：

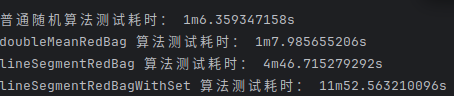
在100000次循环下：

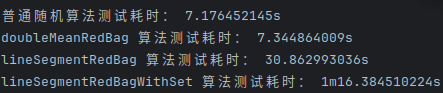
在10000次循环下：