洗牌算法及其测试

前言

之前面试的时候，被问到过洗牌算法，当时没有了解过洗牌算法，所以是按自己的理解去回答的。今天复盘的时候，发现当时面试说的洗牌算法是错误的。

下意识的实现

for循环一次，然后随机交换两个数。

func shuffleArrayGeneral(nums []byte) []byte {
	n := len(nums)
	rand.NewSource(time.Now().UnixNano())
	for i := 0; i < n; i++ {
		a := rand.Intn(n)
		b := rand.Intn(n)
		nums[a], nums[b] = nums[b], nums[a]
	}
	return nums
}

简单跑几次感觉没问题

测试

现在，我们知道洗牌算法应该是应该随机函数，也就是说，我每张牌出现在各个位置上的概率应该是 1 / 牌数。
概率问题，我们只能采用统计的方法来做测试。也就是说，你调用rand()函数100次，其中，每个数出现的次数大约都在 [5,15] 次。

那么接下来，对我前面的洗牌函数进行测试。

在1000000次测试中

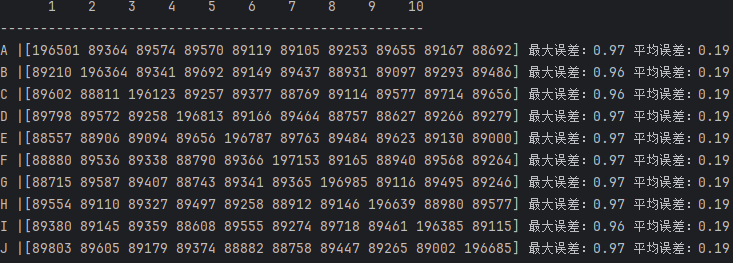
注意看对角线的数据和误差数据，我们会发现之前的算法不能达到我们预期的效果。

Fisher-Yates 洗牌算法

使用一个倒序的循环来进行洗牌操作。循环变量i从n-1开始，递减到0。在每次迭代中，我们将当前位置i的元素与一个随机位置j的元素进行交换

func shuffleArrayFisherYates(nums []byte) []byte {
	n := len(nums)
	rand.NewSource(time.Now().UnixNano())
	for i := n - 1; i >= 0; i-- {
		j := rand.Intn(i + 1)
		nums[i], nums[j] = nums[j], nums[i]
	}
	return nums
}

在1000000次测试中

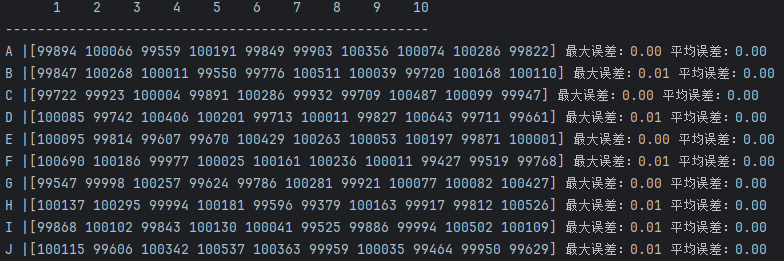
我们能够明显得看到每张牌在各个位置上出现的概率都较为接近。